Page 49 - Полный_курс_физики_с_кратким_обзором_метеорологических_явлений_пер_с_фр

30 Т Я Ж Е С Т Ь .

прнмемъ за единицу длины, т. е. нредположнмъ его равиымъ 1, то мы найдемъ, что
а'С — 4, а"С" = 9, а"! С'"- = 16. Другпмл словами — пространства aG, а 0', а" С"...
1
возрастают соотвѣтственно квадратамъ вроменъ. Эта зависимость можѳтъ быть выра-
а;ена слѣдугоіщшъ образомъ: разстояпія точекъ кривой отъ перпендикуляра, провеЗен-
паого къ оси чррезъ ея вершину, пропорпгопалым квадра­
тамъ разстояній этихъ точекъ отъ самой оси. Этпмъ гео-
метрпческимъ свойствомъ характеризуется кривая, назы­
ваемая параболой. Такимъ
образомъ діаграмма паде-
ігія представлнетъ собою
часть параболы; точка m
составляетъ ея вершину,
прямая тХ, направленіс
равномѣрио ускорнтельна-
го движенія^—ея ось н пря­
мая і«Г, паирав.теиіе рав-
номѣрнаго дппжепіл, есть
касательная къ вершпнѣ.
Этими соображеніями поль­
зуются для точпаго опредѣ-
лепія кривой, 'которая ос­
тается всегдапеопредѣлен-
Рпс. 34. Рпс. 35. ной. Для этого стоить толь­
ко воспользоваться одпимъ
пзъ геометрпчеекпхъ свойствъ параболы. Если провести касательиыя къ двумъ точ-
камъ крпвоіі с' и с " (рис. 35) п возстановить къ ннмъ. перпендикуляры въ точ-
:
кахъ пересѣчеиія съ касательного къ всршпнѣ кривой, то нолученпыя прямыл
пересѣкутся въ одной и той же точкѣ оси, которая будетъ фокусомъ параболы.
Если опустить нзъ этой точкн перпендикуляръ на касательную къ верншиѣ, то
точка пересѣчепія п будетъ вершпною кривой, a слѣдовательно исходной точкою пути
двпженія.
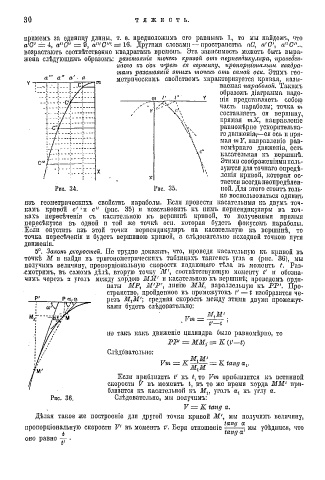
5°. Законъ .скоростей. Пе трудно доказать, что, проведя касательную къ кривой въ
точкѣ M п найдя въ трнгонометрическихъ таблнцахъ тангепсъ угла а (рис. 36), мы
получимъ величину, пропорціональную скорости падающаго гЬла въ момептъ t. Раз-
.смотрпмъ, въ само"мъ дѣлѣ, вторую точку М', соотвѣтствующую моменту V и обозпа-
чпмъ черезъ я ѵголъ между хордою ММ' и касательпою къ вершинѣ; проводемъ орди­
наты MP, М'Р', линію ММ, параллельцую къ РР'. Про­
странство, пройденное въ промежутокъ V — t изобразится че­
резъ M tM'; средняя скорость между этими двумя промежут­
ками будетъ слѣдовательно:
Ѵт z=
t'—t
но такъ какъ двшкеніе цилиндра было равномѣрно, то
РР' = ММ І = К (і'—t)
Слѣдовательно:
Vm = К —— - : К tang a v
Если приблизить V къ £, то Ѵт приблизится къ истинной
скорости V въ момента і, въ то же время хорда ММ 1 при­
близится къ касательной къ М и уголъ a t къ углу а.
Рис. 36. Слѣдовательно, мы получимъ:
V = К tang а.
Дѣлая такое же построеніе для другой точки кривой Ж ' , мы получимъ величину,
пропорціональную скорости V въ момента і'. Беря отпошеиіе мы убѣдпмся, что
оно равно — •